複数の案の中からもっとも得する案の選び方

【考え方】

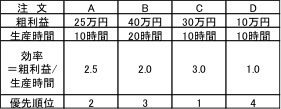
まず、この例題の効率を求めます。効率は、生産時間当たりの粗利益になります。

 

（一般的な効率の算式）

効率＝効果の量／制約された資源の投入量

（この例題の効率の算式）

効率＝粗利益／生産時間

 

効率を使って表を整理しなおすと、次のとおりになります。

 

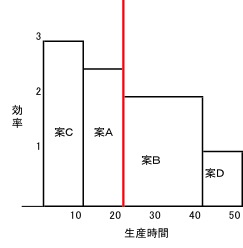
効率からみると注文ＡからＤの中から採用する優先順位は、Ｃ→Ａ→Ｂ→Ｄの順になります。

稼動可能な生産時間は20時間ですから、粗利益を最大化するために選択される案は、Ｃ（10時間）とＡ（10時間）になり、粗利益の合計は55万円（30万円＋25万円）となります。

 

これを図示すると次のようになります。

【例題２】

ハラシマさんは、今、自由に使えるお金を12万円持っていて、誰かに貸付けすることで一儲けしたいと思っています。そこで、知り合いに相談したところ、３つの案件があることを聞きました。

 

《案１》１万円を貸すと翌月3,000円利息を払って返済してくれる

《案２》２万円を貸すと翌月5,000円利息を払って返済してくれる

《案３》３万円を貸すと翌月6,000円利息を払って返済してくれる

 

ハラシマさんは、この３案のうち、どの案を選択すると、儲けを最大にすることができるでしょうか？

ちなみに、この３案は１人あたりの貸付額であって、複数の人からのニーズがあり、借りたい人全ての金額を合計すると12万円をはるかに超えます。

また、あくまで例題なので取引慣行とか金利水準は無視してください。

 

【考え方】

この場合、３案を組み合わせのではなく、３案から一番得な案にお金を全額投入することが儲けを最大にします。

では、一番得なのはどれなのでしょうか。ここでの効率は「利率」になります。

12万円を貸すことができる人数、貸付額の合計、利子の合計について整理すると、次の表のとおりになります。

 

表を見ると一目瞭然ですが、利率（効率）が一番高い案1を採用した場合、利子合計（＝儲け）が一番となります。

 

「独立案」での、一番得な案を選択する考え方をご理解いただけましたでしょうか？

効率を求めることで、複数の案を比較することが容易になり、一番得な案を求めることができました。

 

これまで紹介してきた２案による「比較の原則」とはちょっと毛色が違いますよね。
わかりづらい部分もあると思いますが、他にも複数案から選択する法則はありますので、次回解説することにしましょう。