複数の案から一つしか選べない場合はどう考えればいいか？

【例題２】

凸凹テックでは、自社開発したドーナツ製造機を使い期間限定で、とある観光地に小さなショップを開店します。店員としてバイトを雇う予定ですが、店のサイズは決まっていません。
事前のリサーチでは店の大きさに応じて、売上げ、利益ともに増加することが見込まれています。
 
選択肢として3案が考えられ、想定される店の規模から店員の数は1～3名で、それぞれ売上から材料費や加工費を差し引いた粗利は、以下のとおりになります。
 

さて、営業期間中に支払うバイト代が店員1人あたり20万円とすると、このショップの営業利益が最大になる店員数は何名になるでしょうか。

【考え方】

3案の中から1案選ぶ、まさにこれは排反案から選択です。
 
まずは素直に3案の営業利益（正味利益）から比較してみましょう。

案1　50万円　－　18万円　＝　32万円

案2　84万円　－　36万円　＝　48万円

案3　96万円　－　60万円　＝　36万円

案2の営業利益が48万円となり、利益額が最大になります。よって、正解は、店員数2名となります。ちなみに、この解法のアプローチは、「正味利益」による解法です。

ではもう一つの解法として「追加効率」を紹介しましょう。これは、粗利の増加分＝差額の効率（追加効率）と人件費の追加分（20万円）と比較して損得を判断します。
 

2案の比較において、店員を追加した場合の一人あたりの粗利と人件費をそれぞれの案と比較して損得を見ます。
この例題では、案2までは、人件費の追加分（一人あたり）20万円より粗利の増加分（＝追加効率）が上回っているので有利＝採用と判断します。
 
一方、案3は人件費の増加分より追加効率が12万円で下回っているので不利＝不採用となります。
よって、案2が追加効率の限界なので、正味利益と同様に案2が正解になります。

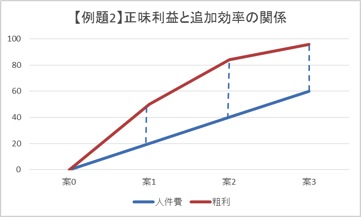
この2つの解法を比較したイメージ図は以下のとおりになります。
粗利と人件費の差額、即ち3案の点線の部分を比較したものが正味利益による解法、粗利と人件費の傾きを比較したものが追加効率による解法となります。
 

 
今回のご説明は以上になります。
 
追加効率の考え方は、排反案以外の複数案からの選択にも応用がきき、様々な不確実性下における分析に対応できますので、次回以降も、具体的な数値を使って、引き続き解説させていただきます。